(ResNet) Deep residual learning for image recognition 번역 및 추가 설명과 Keras 구현

Paper Information

HE, Kaiming, et al. “Deep residual learning for image recognition”. In: Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. p. 770-778.

a.k.a. ResNet paper

---

Abstract

보다 깊어진 뉴럴 네트워크는 학습하기가 더욱 어려워진다. 이 논문에서는 이전 연구들에서 사용 된 네트워크들 보다, 훨씬 깊어진 네트워크의 학습을 용이하게 하기 위한 “Residual Learning Framework”를 제안한다.

여기서 제안하는 방법은 unreferenced function을 학습하는 대신, layer의 input을 참조하는 residual function을 학습하도록 layer를 명시적으로 reformulation한다.

즉, 제안하는 방법은 residual function은 layer의 input를 참조(reference)하도록 구성했기 때문에 referenced function으로 구분했으며, 반면 어떤 값을 참조하지 않는 기존의 일반적인 layer를 unreferenced function으로 구분하고 있다.

정보를 참조하는 방법은 흔히들 “skip connection”으로 알고 있는 구조를 사용하며, 본문에서는 “shortcut connection”으로 설명하고 있다.

제안하는 방법을 적용한 residual network는 optimize하기도 쉬우며, 상당히 깊은 네트워크의 경우에도 합리적인 정확도를 얻어낼 수 있음을 실험 결과로 보여준다.

본문의 실험 파트에서도 언급 될 예정이지만, 극도로 깊어진 네트워크(1000-layer 이상)의 경우에는 상대적으로 얕은 네트워크보다 높은 테스트 오류율을 보인 실험 결과도 있다.

152개의 layer로 구성된 residual network를 Imagenet dataset에서 평가했다. 두 개의 모델을 앙상블 한 결과 ImageNet test set에서 3.57%의 top-5 error를 보였고, ILSVRC 2015 classification 부문에서 1위를 차지했다.

이는 ResNet이 참가했던 ILSVRC 2015의 전년도 대회(ILSVRC 2014)에서 2위를 했던 VGG-19보다 8배나 깊어진 것이다. 당시의 1위는 GoogLeNet(22-layer)이었지만, 이 논문에서는 상대적으로 구조가 간단한 VGG를 기준 모델로 삼고있다.

실험 파트에서는 CIFAR-10에 대한 실험 결과 및 극도로 깊어진 네트워크(1000-layer 이상)에 대한 분석 결과도 보인다.

representation의 깊이는 다양한 visual recognition task에서 매우 중요한 요소이다. residual network로부터 얻어낸 deep representation으로부터 COCO object detection dataset에서 28%의 성능 향상을 얻었으며, ImageNet detection/localization, COCO detection/segmentation 부문에서 1위를 차지했다.

representation은 네트워크의 각 layer들을 거친 결과로 생각하면 된다. 즉, 보다 많은 layer로부터 추출된 고차원의 feature일수록 양질의 정보를 가진다는 것으로 생각할 수 있다.

---

1. Introduction

Deep network는 low/mid/high-level feature와 classifier를 end-to-end multi-layer 방식으로 자연스럽게 통합해주며, 각 feature들의 소위 ‘level’은 해당 feature를 추출하기 위해 거친 layer의 depth에 따라 달라진다. ImageNet에서의 주요 결과들은 모두 depth가 16~30 정도인 ‘very deep’ model을 이용했으며, 다른 visual recognition task에서도 ‘very deep’ model이 큰 도움이 됐다.

논문이 작성될 당시 기준으로 16~30 layer(ILSVRC 2014)는 그 이전(~8 layer, ~ILSVRC 2013)에 비해 상당히 깊어진 모델이다.

Depth의 중요성이 부각되며, ‘Is learning better networks as easy as stacking more layers?’와 같은 궁금증이 생겨났다. 여기에는 초기 단계에서부터 수렴을 방해하는 vanishing/exploding gradient라는 문제가 있었지만, ‘normalized initialization’과 ‘intermediate normalization’ 기법의 연구를 통해 대부분 해결됐다.

두 기법 중, 전자는 xavier/he initialization 등으로 잘 알려진 ‘weight initialization’ 기법으로 생각하면 되고, 후자는 ‘batch normalization’을 생각하면 된다.

각 해결책을 통해 deep network가 수렴하게 되면, 또 다른 성능 저하 문제가 드러난다. 이는 네트워크의 depth가 증가하면서 정확도가 포화상태에 도달하게 되면 성능이 급격하게 떨어지는 현상을 말한다. 이 문제는 overfitting으로 인한 것이 아니며, depth가 적절히 설계된 모델에 더 많은 layer를 추가하면 training error가 커진다는 이전 연구 결과에 기반한다. 아래 Fig.1에서는 간단한 실험을 통해 성능 저하 문제를 보여준다.

Fig.1
20-layer와 56-layer를 가진 두 plain network가 CIFAR-10 dataset을 학습했을 떄의 training error(왼쪽)와 test error(오른쪽)를 나타낸다.

Depth가 더 깊을 수록 training error가 높았으며, 이에 따라 test error도 높게 나타난다. ImageNet에 대한 학습에서도 유사한 현상이 나타났다. (Fig.4)

이와 같은 성능 저하 문제는, 모든 시스템의 최적화 난이도가 비슷한 것이 아님을 시사한다.

shallower architecture와 더 많은 layer를 추가한 deeper architecture를 고려하자. 일반적으로 deeper model에 대해서는 최소 shallower model 이상의 성능을 기대할 것이다. 이를 만족하는 deeper architecture를 위한 constructed solution이 있긴 하다. 기존에 학습된 shallower architecture에다가 identity mapping인 layer만 추가하여 deeper architecture를 만드는 방법이다. 하지만, 실험을 통해 현재의 solver들은 이 constructed solution이나 그 이상의 성능을 보이는 solution을 찾을 수 없다는 것을 보여준다.

기존의 shallower model에서 입력이 x일 때의 출력을 S(x)라고 할 때, deeper model을 구성하기 위해 이 모델의 상단에 추가되는 layer들이 모두 identity function과 같이 동작을 한다면(즉, 입력이 x일 때, layer의 출력 L(x)가 x인 경우) deeper model의 출력 D(x)는 S(x)와 동일하다.

현재의 solver라는 것은 받아들인 데이터로부터 네트워크를 학습하는 알고리즘을 뜻한다. 즉, 현재의 optimizer(본문에서는 SGD만을 사용하는 것으로 보임)로는 deeper model로부터 shallower model의 성능을 이끌어는 것조차 못한다는 것을 실험 결과로 보여준다.

이 논문에서는 “Residual Learning Framework”를 도입하여 성능 저하 문제를 해결하고 있다. 이 방법은 few stacked layer를 underlying mapping을 직접 학습하지 않고, residual mapping에 맞추어 학습하도록 한다. underlying mapping 즉, 원래의 original mapping을 H(x)로 나타낸다면, stacked nonlinear layer의 mapping인 F(x)는 H(x)-x 를 학습하는 것이다. 따라서 original mapping은 F(x)+x 로 재구성 된다.

stacked layer 혹은 stacked nonlinear layer는 추가 된 layer라고 생각하면 된다(Fig.2 building block 참조). 이 때, 추가된 layer들을 H(x)-x에 맞추어 학습하지만, 각 layer는 결국 H(x)를 근사하는 것이 목적이므로, F := H(x)-x를 H(x)에 대한 식으로 전개하여 original mapping이 F(x)+x 로 재구성 된 것으로 볼 수 있다.

또한, 저자들은 unreferenced mapping인 original mapping보다, referenced mapping인 residual mapping을 optimize하는 문제가 더 쉽다고 가정한다. 극단적으로 H(x)에 대한 optimal solution이 identity mapping이라는 가정을 한다면, H(x)의 결과를 x가 되도록 학습하는 것보단, F(x)가 0이 되도록 학습하는 것이 쉬울 것이라는 직관에 따른 가정이다.

H(x)=F(x)+x이기 때문에, H(x)=x가 되도록 한다는 것은 F(x)+x를 x가 되도록 학습한다는 뜻이다. 즉, residual(입력 x와의 잔차)인 F(x)가 0이 되는 것이 본 가설에서의 optimal solution인 identity mapping이 되는 것이다.

F(x)+x는 “shortcut connection”으로 구현할 수 있다. shortcut connection은 하나 이상의 layer를 건너 뛴다. 본문에서 shortcut connection은 identity mapping을 수행하고, 그 출력을 stacked layer의 출력에 더하고 있다. 아래 Fig.2는 residual learning을 위한 building block 구조를 보여준다.

Fig.2
입력 x가 2개의 stacked layer를 거친 결과(ReLU 이전)와 identity인 입력 x를 더한 후에 nonlinearity layer(ReLU)를 통과한다.

이와 같은 identity shortcut connection은 별도의 parameter나 computational complexity가 추가되지 않는다. 이를 이용한 네트워크는 SGD에 따른 역전파로 end-to-end 학습이 가능하며, solver 수정 없이도 common library를 사용하여 쉽게 구현할 수 있다. (ex, Caffe 등)

152개의 layer로 구성된 residual network가 19개의 layer로 구성된 VGG-19보다 낮은 computational complexity를 가진다고 한다.

이 글의 후반부에는 keras에서 shortcut connection을 간단하게 구현한 코드를 추가해뒀다.

이 논문에서는 ImageNet에 대해 다음 두 실험의 결과를 제공한다.

1. plain network(simply stack layers)는 depth가 깊어짐에 따라 더 높은 training error를 보이는 것에 반해, 제안한 deep residual network는 쉽게 최적화가 가능함.
2. 또한, deep residual network는 아주 깊어진 depth에서 성능의 이득을 가졌으며, 이전에 연구됐던 네트워크에 비해 훨씬 향상된 결과를 보임.

또한, CIFAR-10 dataset에 대해서는 다음 실험의 결과를 제공한다.

1. 성능 저하 문제 및 제안하는 방법의 효과가 특정 dataset(ImageNet)에만 국한되지 않음을 보임
2. 제안하는 방법의 사용 여부에 따른 layer response의 std 분석
3. 1000개 이상의 layer로 이루어진 모델에 대한 실험

---

3. Deep Residual Learning

3.1 Residual Learning

1장에서 설명한 바와 같이, stacked layer를 H(x)-x에 mapping함으로써 original mapping을 F(x)+x로 reformulation하는 것은, 성능 저하 문제를 해결하기 위함이다.

실제 상황에서 H(x)의 optimal이 identity mapping이 아닐지라도, 이 reformulation은 문제에 precondition을 제공하는 효과를 준다. 만약 optimal function이 zero mapping보다 identity mapping에 더 가깝다면, solver가 identity mapping을 참조하여 작은 변화 F(x)를 학습하는 것이 새로운 function을 생으로 학습하는 것보다 쉬울 것이다. 실험에서는 학습된 residual function에서 일반적으로 작은 반응이 있다는 결과를 보여준다(Fig.7 참조). 이 결과는 identity mapping이 합리적인 preconditioning을 제공한다는 것을 시사한다.

H(x)의 optimal이 identity라는 것은 shallower model의 성능이 depth의 증가로 얻을 수 있는 성능의 상한이 된다는 말로, 모델의 depth에 대한 일반적인 상식과 반대되는 결과이다.

reformulation한 식 F(x)+x는 identity mapping이 optimal일 경우를 가정하여 구성한 것으로 보인다. 그러나, 이는 가정일 뿐 실제로 depth가 깊어질수록 성능의 향상을 기대하는 경우엔 H(x)의 optimal이 identity라고 보기 어렵다. 그럼에도 F(x)+x라는 식에서는 입력 x가 학습 시에 일종의 guide로써 작용하여 학습을 도와주므로, identity가 optimal이 아닌 경우라도 이 reformulation은 여전히 긍정적인 효과를 기대할 수 있는 것이다.

3.2 Identity Mapping by Shortcuts

이 논문에서는 few stacked layers마다 residual learning을 사용한다. 그 building block은 위의 Fig.2에서 보였으며, 논문에서는 이를 Eqn.1과 같이 정의했다.

Eqn.1

y = F(x, {W_i}) + x

x와 y는 각각 building block에서 input과 output이다. F(x, {W_i})는 학습 되어야 할 residual mapping을 나타낸다. Fig.2와 같이 layer가 두 개 있는 경우를 예로 들면, F = W₂σ(W₁x)로 나타낼 수 있다. 여기서 σ는 ReLU를 나타내며, bias는 표기법 간소화를 위해 생략된다. F + x 연산은 shortcut connection 및 element-wise addition으로 수행되며, addition 후에는 second nonlinearity로 ReLU를 적용한다.

1장에서도 언급했지만, Eqn.1의 shortcut connection 연산은 별도의 parameter나 computational complexity가 추가되지 않는다. 이 특징은 plain network와 residual network 간의 공정한 비교를 가능하게 해준다.

element-wise addition 연산은 무시해도 될 정도이므로 공정한 요소로 인정한다.

Eqn.1에서 F + x 연산은 둘의 dimension이 같아야 하며, 이를 위해 linear projection W_s을 수행할 수 있다. 이는 Eqn.2와 같이 정의된다.

Eqn.2

y = F(x, {W_i}) + W_sx

또한, Eqn.1에서 square matrix인 W_s를 사용할 수도 있다. 하지만, 성능 저하 문제를 해결하기에는 identity mapping만으로도 충분하고 경제적이라는 것을 실험에서 보여준다. 따라서 W_s는 dimension matching의 용도로만 사용한다.

identity인 x를 mapping하기 전 feature를 한 번 더 추출하는 layer를 거친 후에 mapping 할 수도 있다는 뜻으로 보인다. 하지만 이렇게 하지 않아도 성능 저하 문제를 해결하기엔 충분하기 때문에 W_sx는 단순히 F와의 dimension matching을 위한 연산일 뿐이다.

위 식은 표기법 간소화를 위해 FC layer 상에서 표현한 것이며, conv layer 상에서도 마찬가지로 identity mapping을 구현할 수 있다. 이 경우에는 dimension matching을 위해 1x1 filter의 conv layer를 이용하며, element-wise addition은 feature map 간의 channel-by-channel addition으로 수행된다.

Projection은 현재 데이터와 다른 차원에서 보기 위한 것으로 생각하면 된다. FC layer 상에서 이 projection이 필요한 경우는 다음과 같다.

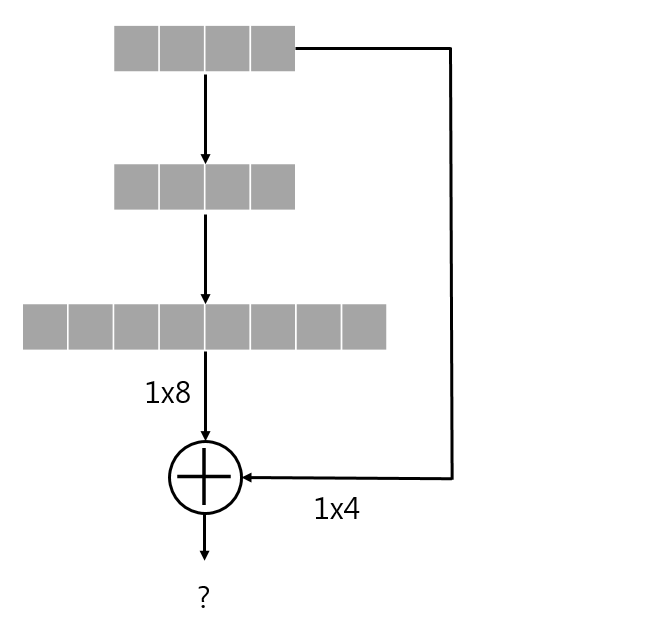
shortcut을 통해 출력과 2-layer 전의 입력의 dimension이 달라, addition이 불가능하다.

위의 unmatched dimension 문제를 해결하기 위해 projection 과정을 추가하는 것은 다음과 같은 과정으로 볼 수 있다.

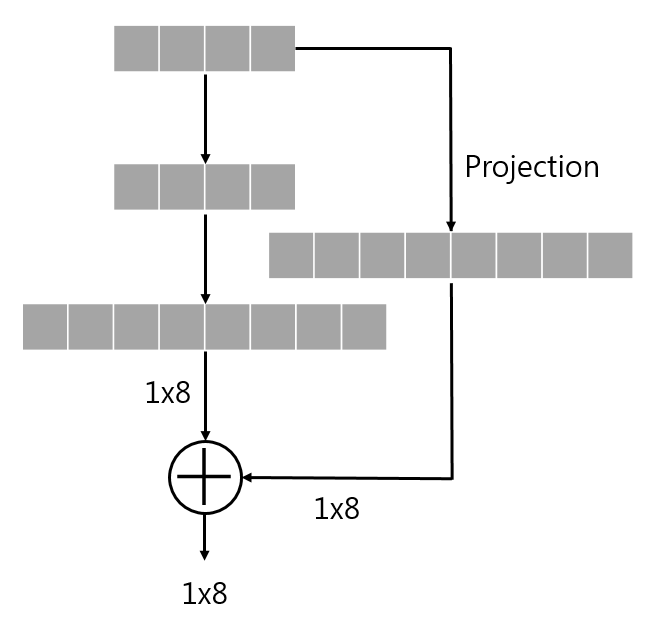
projection 과정을 통해 둘의 dimension을 맞춘 후에 addition을 진행한다.

FC layer 상에서는 이와 같이 node의 개수만 맞추면 되지만, conv layer의 경우에는 feature map size와 channel의 개수까지 맞춰야 한다.

residual function인 F의 형태는 유연하게 결정할 수 있다. 즉, 본문에서는 2~3개의 layer가 포함된 F를 사용하지만, 더 많은 layer를 포함하는 것도 가능하다. 하지만, F가 하나의 layer만 갖는 경우에는 별도의 advantage를 측정하지 못했으며, 단순 linear layer와 유사한 것으로 보인다.

3.3 Network Architectures

이 논문에서는 다양한 형태의 plain/residual network에 대해 테스트 했으며, 일관된 현상을 관찰한다. 실험에서 ImageNet dataset을 위한 두 모델을 다음과 같이 정의했다.

Plain network
baseline은 주로 VGG net(Fig.3 왼쪽)의 철학에 영감을 받았다. conv layer는 대개 3x3 filter를 가지며, 두 가지의 간단한 규칙에 따라 디자인 된다.

1. 동일한 output feature map size에 대해, layer는 동일한 수의 filter를 갖는다.

2. feature map size가 절반 인 경우, layer 당의 time complexity를 보전하기 위해 filter의 수를 2배로 한다.

downsampling 시에는 strides가 2인 conv layer를 사용했으며, 네트워크의 마지막에는 GAP와 activation이 softmax인 1000-way FC layer로 구성된다. 이 plain network는 VGG-19에 비해 적은 수의 filter와 낮은 complexity가 가진다.

34개의 layer로 구성된 이 baseline plain network(Fig.3 가운데)는 3.6 billion FLOPs이며, 이는 VGG-19(19.6 billion FLOPs)의 18%에 불과하다.

Residual network
위 plain network를 기반으로, shortcut connection을 삽입하여 residual version의 network를 만든다. (Fig.3 오른쪽)

identity shortcut(Eqn.1)은 input과 output이 동일한 dimension인 경우(Fig.3의 solid line shortcuts)에는 직접 사용될 수 있으며, dimension이 증가하는 경우(Fig.3의 dotted line shortcuts)에는 아래의 두 옵션을 고려한다.

1. zero entry를 추가로 padding하여 dimension matching 후 identity mapping을 수행한다. (별도의 parameter가 추가되지 않음)

2. Eqn.2의 projection shortcut을 dimension matching에 사용한다.

shortcut connection이 다른 크기의 feature map 간에 mapping될 경우, 두 옵션 모두 strides를 2로 수행한다.

feature map의 크기가 달라지는 경우는 strides가 2인 conv layer를 통한 downsampling을 거쳤기 때문이다.

Fig.3
ImageNet dataset 학습에 사용된 network architecture

왼쪽은 VGG-19 model (19.6 billion FLOPs)
가운데는 34-layer plain network (3.6 billion FLOPs)
오른쪽은 34-layer residual network (3.6 billion FLOPs)

dotted shortcut은 dimension이 증가한 결과와 mapping하는 경우이다.

3.4 Implementation

논문에서 ImageNet dataset에 대한 실험은 AlexNet과 VGG의 방법을 따른다. 이미지는 scale augmentation를 위해 [256, 480]에서 무작위하게 샘플링 된 shorter side를 사용하여 rescaling된다. 224x224 crop은 horizontal flip with per-pixel mean subtracted 이미지 중에 무작위로 샘플링 되며, standard color augmentation도 사용된다.

언급된 기법(horizontal flip, per-pixel mean subtract, standard color augmentation)들로 data augmentaion을 수행하여 학습한다는 말이다.

• 각각의 conv layer와 activation 사이에는 batch normalization을 사용하며, He initialization 기법으로 weight를 초기화하여 모든 plain/residual nets을 학습한다.

• batch normalization에 근거해 dropout을 사용하지 않는다.

• learning rate는 0.1에서 시작하여, error plateau 상태마다 rate를 10으로 나누어 적용하며, decay는 0.0001, momentum은 0.9로 한 SGD를 사용했다.

• mini-batch size는 256로 했으며, iteration은 총 600K회 수행된다.

비교를 위해 AlexNet의 standard 10-crop test를 수행했다. 최상의 결과를 내기 위해, VGG와 He initialization에서 사용한 fully-convolutional form을 적용했으며, multiple scale에 대한 score를 평균했다.

fully-convolutional form은 정적인 크기를 가지는 FC layer를 제외하여 다양한 크기의 입력을 처리할 수 있는 방법이다. 자세한 설명은 OverFeat논문을 참조하자. VGG와 He initialization 둘 다 이 논문의 방법을 사용한다.

multiple scale은 shorter side가 {224, 256, 384, 480, 640}인 것으로 rescaling하여 사용한다.

---

4. Experiments

4.1 ImageNet Classification

논문에서는 1000개의 class로 구성 된 ImageNet 2012 classification dataset에서 제안하는 방법을 평가했다. 모델의 학습 및 테스트에 사용된 training/validation/test 이미지의 개수는 각각 1.28M/50K/100K개에 해당한다. 테스트 결과는 top-1 error와 top-5 error를 모두 평가한다. 실험에 사용된 각 네트워크의 상세 비교는 4.1절의 마지막에 삽입된 Table.1을 참조하자.

Plain Networks
우선 18-layer 및 34-layer plain network를 평가한다. 34-layer plain network는 Fig.3의 가운데와 같으며, 18-layer는 이와 유사한 형태로 구성 된다. Table.2의 결과에서는 18-layer network에 비해, 34-layer network의 validation error가 높은 것으로 보인다.

이유를 알아보기 위해 Fig.4의 왼쪽 그래프에서 학습 중의 training/validation error를 확인해보자. 18-layer plain network의 solution space는 34-layer plain network의 subspace임에도 불구하고, 오히려 34-layer인 경우의 error가 학습 과정 전반에 걸쳐서 더 높게 나타나는 성능 저하 문제를 관찰할 수 있다.

Fig.4
ImageNet dataset을 학습하는 동안의 training/validation error 추이를 나타낸 그래프이다. 왼쪽은 18-layer 및 34-layer plain network에 대한 error를 나타낸 것이며, 오른쪽은 각각 같은 layer수를 지닌 residual network에 대한 error를 나타낸 것이다. 얇은 곡선과 굵은 곡선은 각각 training error와 validation error를 나타낸다.

논문의 저자들은 여기서 직면하는 optimization difficulty가 vanishing gradients에 의한 것 같지는 않다고 주장한다. 그 이유는, 이 plain network가 batch normalization을 포함하여 학습했기 때문에 forward propagated signal의 분산이 0이 아니도록 보장됐으며, backward propagated gradients가 healty norm을 보이는 것도 확인했기 때문이다. 따라서 forward/backward signal은 vanishing 하지 않았다고 볼 수 있다.

Table.3의 결과를 따르면 34-layer plain network가 여전히 경쟁력 있는 정확도를 달성했으며, 이는 solver의 작동이 이루어지긴 한다는 것을 의미한다. 저자들은 또한, deep plain network는 exponentially low convergence rate를 가지며, 이것이 training error의 감소에 영향 끼쳤을거라 추측하고 있다.

저자들은 훨씬 많은 iteration을 수행해봤지만 여전히 성능 저하 문제가 관찰됐다고 한다. 이는 이 문제가 단순한 반복 학습으로 해결가능한 것이 아님을 시사한다.

Residual Networks
다음으로 18-layer 및 34-layer residual network(이하 ResNet)를 평가한다. baseline architecture는 위의 plain network와 동일하며, Fig.3의 오른쪽과 같이 각 3x3 filter pair에 shortcut connection을 추가했다. 모든 shortcut connection은 identity mapping을 사용하며, dimension matching을 위해서는 zero-padding을 사용한다(3.3절의 옵션 1 참조). 따라서, 대응되는 plain network에 비해 추가되는 parameter가 없다.

Table.2와 Fig.4에서 알 수 있는 3가지 주요 관찰 결과는 다음과 같다.

1. residual learning으로 인해 상황이 바뀌었다. 34-layer ResNet이 18-layer ResNet보다 우수한 성능을 보인다. 또한, 34-layer ResNet이 상당히 낮은 training error를 보였으며, 이에 따라 향상된 validation 성능이 관측됐다. 이는 성능 저하 문제가 잘 해결됐다는 것과, 증가된 depth에서도 합리적인 accuracy를 얻을 수 있다는 것을 나타낸다.

2. 34-layer ResNet은 이에 대응하는 plain network와 비교할 때, validation data에 대한 top-1 error를 3.5% 줄였다(Table.2 참조). 이는 extremely deep systems에서 residual learning의 유효성을 입증하는 결과다.

3. 18-layer plain/residual network 간에는 유사한 성능을 보였지만, Fig.4에 따르면 18-layer ResNet이 더욱 빠르게 수렴한다. 이는 network가 “not overly deep”한 경우(18-layers의 경우), 현재의 SGD solver는 여전히 plain net에서도 좋은 solution을 찾을 수 있다는 것으로 볼 수 있다. 하지만, 이러한 경우에도 ResNet에서는 빠른 수렴속도를 기대할 수 있다.

Table.2
학습 된 18-layer 및 34-layer plain/residual network의 validation data에 대한 10-crop testing 결과 중 top-1 error를 나타낸 표다.

Identity vs. Projection Shortcuts
앞에서 parameter-free한 identity shortcut이 학습에 도움 된다는 것을 보였다. 이번에는 Eqn.2의 projection shortcut에 대해 조사하자. Table.3에서는 다음 3가지 옵션에 대한 결과를 보여준다.

1. zero-padding shortcut는 dimension matching에 사용되며, 모든 shortcut는 parameter-free하다(Table.2 및 Fig.4의 결과 비교에 사용됨).

2. projection shortcut는 dimension을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity다.

3. 모든 shortcut은 projection이다.

Table.3에서는 3가지 옵션 모두 plain network보다 훨씬 우수함을 보여준다. 옵션 간의 비교를 하자면, 옵션 1보다는 옵션 2가 약간 좋으며, 옵션 2보다는 옵션 3이 약간 더 좋다. 이 때, 옵션 1과 옵션 2의 성능 차이는 zero-padding으로 추가된 dimension에서는 residual learning의 이점을 갖지 못하기 때문이며, 옵션 2와 옵션 3의 성능 차이는 projection shortcut에 의해 추가된 parameter가 성능에 영향을 줬기 때문으로 추정된다.

여기서 3가지 옵션 간의 차이는 미미하다는 사실은 projection shortcut이 성능 저하 문제를 해결하는데 필수적이지 않다는 것을 나타낸다. 따라서 memory/time complexity와 model size를 줄이기 위해 이 논문에서는 옵션 3을 사용하지 않는다. 여기서 얻어지는 이점은 아래에서 소개 될 bottleneck architecture의 complexity를 높이지 않기 위해서도 특히 중요한 요소로 작용한다.

Deeper Bottleneck Architectures
다음으로 ImageNet dataset을 위한 deeper network를 설명한다. 감당할 수 없는 training time에 대한 우려로 인해, building block을 bottleneck design으로 수정한다. 각 residual function F, 2-layer stack대신 3-layer stack을 사용한다(Fig.5 참조). 3개의 layer는 각각 순서대로 1x1, 3x3, 1x1 conv layer이며, 1x1 conv layer는 dimension을 줄이거나 늘리는 용도로 사용하며, 3x3 layer의 input/output의 dimension을 줄인 bottleneck으로 둔다. Fig.5에서는 2-layer stack과 3-layer stack의 디자인을 보여준다. 둘은 유사한 time complexity를 갖는다.

Fig.5
ImageNet data에 대한 학습을 위한 deeper residual function F의 building block이다. 왼쪽은 Fig.3의 ResNet에서 feature map의 크기가 56x56인 경우의 building block이며, 오른쪽은 ResNet-50/101/152에서 같은 경우에 사용하는 ‘bottleneck’ building block이다.

여기서 parameter-free인 ideneity shortcut은 이 architecture에서 특히 중요하다. 만약 Fig.5의 오른쪽 다이어그램에서 identity shortcut이 projection으로 대체된다면, shortcut이 두 개의 high-dimensional 출력과 연결되므로 time complexity와 model size가 두 배로 늘어난다. 따라서 identity shortcut은 이 bottleneck design을 보다 효율적인 모델로 만들어준다.

50-layer ResNet
34-layer ResNet의 2-layer block들을 3-layer bottleneck block으로 대체하여 50-layer ResNet을 구성했다. dimension matching을 위해서는 위의 옵션 2를 사용한다. 이 모델은 3.8 billion FLOPs 이다.

projection shortcut는 dimension을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity다. (옵션 2)

101-layer and 152-layer ResNets
여기에 3-layer bottleneck block을 추가하여 101-layer 및 152-layer ResNet을 구성했다. depth가 상당히 증가했음에도 상당히 높은 정확도가 결과로 나왔다. depth의 이점이 모든 evaluation metrics에서 발견됐다.

Table.3과 Table.4에서 ResNet의 depth에 따라 일관성 있는 결과를 보여주고 있다.

Table.3
각 수치는 ImageNet validation data에 대한 10-crop testing error를 나타낸다.

Comparisons with State-of-the-art Methods
Table.4에서는 previous best single-model의 성능과 비교한다. 우리의 baseline인 34-layer ResNet은 previous best에 비준하는 정확도를 달성했으며, 152-layer ResNet의 single-model top-5 error는 4.49%를 달성했다. 이 결과는 이전의 모든 ensemble result를 능가하는 성능이다(Table.5 참조). 또한, 서로 다른 depth의 ResNet을 6개 ensemble하여 top-5 test error를 3.57%까지 달성했다. 이는 ILSVRC 2015 classification task에서 1위를 차지했다.

제출 시에는 두 개의 152-layer만 사용했다고 한다.

Table.4
각 수치는 ImageNet validation data에 대한 single-model의 testing error를 나타낸다.

Table.5
각 수치는 ImageNet test data에 대한 ensemble model의 testing error를 나타낸다.

Table.1
ImageNet data에 대한 학습으로 사용 된 각 네트워크의 구조를 나타낸다. conv3_1, conv4_1, conv5_1에서는 strides를 2로 수행하여 Downsampling한다.

keras에서 18-layer plain/residual network를 비교하자면 다음과 같다. 위 실험에서 18-layer의 경우에는 dimension matching을 위해 zero-padding을 이용했었지만, 이 외에는 어차피 projection을 사용하기 때문에 projection으로 구현한다.

def conv2d_bn(x, filters, kernel_size, padding='same', strides=1, activation='relu'):
    x = Conv2D(filters, kernel_size, kernel_initializer='he_normal', padding=padding, strides=strides)(x)
    x = BatchNormalization()(x)
    if activation:
        x = Activation(activation)(x)
    
    return x
    
def plain18(model_input, classes=10):
    conv1 = conv2d_bn(model_input, 64, (7, 7), strides=2, padding='same') # (112, 112, 64)
    
    conv2_1 = MaxPooling2D((3, 3), strides=2, padding='same')(conv1) # (56, 56, 64)
    conv2_2 = conv2d_bn(conv2_1, 64, (3, 3))
    conv2_3 = conv2d_bn(conv2_2, 64, (3, 3))
    
    conv3_1 = conv2d_bn(conv2_3, 128, (3, 3), strides=2) # (28, 28, 128)
    conv3_2 = conv2d_bn(conv3_1, 128, (3, 3))
    
    conv4_1 = conv2d_bn(conv3_2, 256, (3, 3), strides=2) # (14, 14, 256)
    conv4_2 = conv2d_bn(conv4_1, 256, (3, 3))
    
    conv5_1 = conv2d_bn(conv4_2, 512, (3, 3), strides=2) # (7, 7, 512)
    conv5_2 = conv2d_bn(conv5_1, 512, (3, 3))
    

    gap = GlobalAveragePooling2D()(conv5_2)
    
    model_output = Dense(classes, activation='softmax', kernel_initializer='he_normal')(gap) # 'softmax'
    
    model = Model(inputs=model_input, outputs=model_output, name='Plain18')
        
    return model

def ResNet18(model_input, classes=10):
    conv1 = conv2d_bn(model_input, 64, (7, 7), strides=2, padding='same') # (112, 112, 64)
    
    conv2_1 = MaxPooling2D((3, 3), strides=2, padding='same')(conv1) # (56, 56, 64)
    conv2_2 = conv2d_bn(conv2_1, 64, (3, 3))
    conv2_3 = conv2d_bn(conv2_2, 64, (3, 3), activation=None) # (56, 56, 64)
    
    shortcut_1 = Add()([conv2_3, conv2_1])
    shortcut_1 = Activation(activation='relu')(shortcut_1) # (56, 56, 64)

    
    conv3_1 = conv2d_bn(shortcut_1, 128, (3, 3), strides=2)
    conv3_2 = conv2d_bn(conv3_1, 128, (3, 3)) # (28, 28, 128)
    
    shortcut_2 = conv2d_bn(shortcut_1, 128, (1, 1), strides=2, activation=None) # (56, 56, 64) -> (28, 28, 128)
    shortcut_2 = Add()([conv3_2, shortcut_2])
    shortcut_2 = Activation(activation='relu')(shortcut_2) # (28, 28, 128)

    
    conv4_1 = conv2d_bn(shortcut_2, 256, (3, 3), strides=2)
    conv4_2 = conv2d_bn(conv4_1, 256, (3, 3)) # (14, 14, 256)
    
    shortcut_3 = conv2d_bn(shortcut_2, 256, (1, 1), strides=2, activation=None) # (28, 28, 128) -> (14, 14, 256)
    shortcut_3 = Add()([conv4_2, shortcut_3])
    shortcut_3 = Activation(activation='relu')(shortcut_3) # (14, 14, 256)
    
    
    conv5_1 = conv2d_bn(shortcut_3, 512, (3, 3), strides=2)
    conv5_2 = conv2d_bn(conv5_1, 512, (3, 3)) # (7, 7, 512)
    
    shortcut_4 = conv2d_bn(shortcut_3, 512, (1, 1), strides=2, activation=None) # (14, 14, 256) -> (7, 7, 512)
    shortcut_4 = Add()([conv5_2, shortcut_4])
    shortcut_4 = Activation(activation='relu')(shortcut_4) # (7, 7, 512)
    

    gap = GlobalAveragePooling2D()(shortcut_4)
    
    model_output = Dense(classes, activation='softmax', kernel_initializer='he_normal')(gap) # 'softmax'
    
    model = Model(inputs=model_input, outputs=model_output, name='ResNet18')
        
    return model

또한, bottleneck 구조를 채택한 50-layer ResNet을 구현하면 다음과 같다.

def bottleneck_identity(input_tensor, filter_sizes):
    filter_1, filter_2, filter_3 = filter_sizes
    
    x = conv2d_bn(input_tensor, filter_1, (1, 1))
    x = conv2d_bn(x, filter_2, (3, 3))
    x = conv2d_bn(x, filter_3, (1, 1), activation=None)
    
    shortcut = Add()([input_tensor, x])
    shortcut = Activation(activation='relu')(shortcut)
    
    return shortcut

def bottleneck_projection(input_tensor, filter_sizes, strides=2):
    filter_1, filter_2, filter_3 = filter_sizes
    
    x = conv2d_bn(input_tensor, filter_1, (1, 1), strides=strides)
    x = conv2d_bn(x, filter_2, (3, 3))
    x = conv2d_bn(x, filter_3, (1, 1), activation=None)
    
    projected_input = conv2d_bn(input_tensor, filter_3, (1, 1), strides=strides, activation=None)
    shortcut = Add()([projected_input, x])
    shortcut = Activation(activation='relu')(shortcut)
    
    return shortcut

def ResNet50(model_input, classes=10):
    conv1 = conv2d_bn(model_input, 64, (7, 7), strides=2, padding='same') # (112, 112, 64)
    
    conv2_1 = MaxPooling2D((3, 3), strides=2, padding='same')(conv1) # (56, 56, 64)
    conv2_2 = bottleneck_projection(conv2_1, [64, 64, 256], strides=1)
    conv2_3 = bottleneck_identity(conv2_2, [64, 64, 256])
    conv2_4 = bottleneck_identity(conv2_3, [64, 64, 256])# (56, 56, 256)
    
    conv3_1 = bottleneck_projection(conv2_4, [128, 128, 512])
    conv3_2 = bottleneck_identity(conv3_1, [128, 128, 512])
    conv3_3 = bottleneck_identity(conv3_2, [128, 128, 512])
    conv3_4 = bottleneck_identity(conv3_3, [128, 128, 512]) # (28, 28, 512)
    
    conv4_1 = bottleneck_projection(conv3_4, [256, 256, 1024])
    conv4_2 = bottleneck_identity(conv4_1, [256, 256, 1024])
    conv4_3 = bottleneck_identity(conv4_2, [256, 256, 1024])
    conv4_4 = bottleneck_identity(conv4_3, [256, 256, 1024])
    conv4_5 = bottleneck_identity(conv4_4, [256, 256, 1024])
    conv4_6 = bottleneck_identity(conv4_5, [256, 256, 1024]) # (14, 14, 1024)
    
    conv5_1 = bottleneck_projection(conv4_6, [512, 512, 2048])
    conv5_2 = bottleneck_identity(conv5_1, [512, 512, 2048])
    conv5_3 = bottleneck_identity(conv5_2, [512, 512, 2048]) # (7, 7, 2048)

    gap = GlobalAveragePooling2D()(conv5_3)
    
    model_output = Dense(classes, activation='softmax', kernel_initializer='he_normal')(gap) # 'softmax'
    
    model = Model(inputs=model_input, outputs=model_output, name='ResNet50')
        
    return model

dimension이 달라지는 부분에선 projection이 추가되어야 하기 때문에 identity와 구분했다. bottleneck_projection 내부를 보면, 첫 번째 convolution에서 feature map size를 줄이기 위해 strides=2를 사용하며, shortcut에서도 이를 맞추기 위해 strides=2를 사용한다. conv2_2에서 strides=1을 사용하는 이유는 이미 MaxPooling2D를 거쳐 feature map size가 줄어든 상태이기 때문이다.

위 ResNet50은 keras에서 제공하는 application model 코드와 비교해도 큰 차이가 없다.

위에서 정의한 모델들을 ImageNet dataset 대신 224x224 크기로 resize한 CIFAR-10 dataset에 적용하는 전체 코드는 다음과 같다. 학습에 사용된 hyperparameter는 3.4절의 방법을 따르며, data augmentation은 하지 않는다.

from keras.models import Model, Input
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D, Activation, Dense, BatchNormalization
from keras.layers import Add
from keras.optimizers import SGD
from keras.callbacks import ReduceLROnPlateau

from keras.utils import to_categorical
from keras.datasets import mnist, cifar10
import numpy as np

def Upscaling_Data(data_list, reshape_dim):
    ...
    
def conv2d_bn(x, filters, kernel_size, padding='same', strides=1, activation='relu', name='default'):
    ...

def plain18(model_input, classes=10):
    ...

def ResNet18(model_input, classes=10):
	...

def bottleneck_identity(input_tensor, filter_sizes):
    ...

def bottleneck_projection(input_tensor, filter_sizes, strides=2):
	...
    
def ResNet50(model_input, classes=10):
	...


class stop_on_iteration(Callback):   
    def __init__(self, iteration=1):
        self.cnt_batch = 0
        self.iteration = iteration
        super(Callback, self).__init__()
        
    def on_batch_end(self, batch, logs={}):
        self.cnt_batch += 1
        if self.cnt_batch == self.iteration:
            self.model.stop_training = True
            
    def on_epoch_end(self, epoch, logs={}):
        if self.model.stop_training:
            if len(self.validation_data):
                import keras.backend as K
                from keras.losses import categorical_crossentropy
                from keras.metrics import categorical_accuracy
                x_val = self.validation_data[0]
                y_val = self.validation_data[1]
                pred = self.model.predict(x_val)

                val_loss = np.mean(K.eval(categorical_crossentropy(K.constant(y_val), K.constant(pred))))
                val_acc = np.sum(K.eval(categorical_accuracy(K.constant(y_val), K.constant(pred))))/len(x_val)
            
            print('\n\nloss: %.4f - acc: %.4f - val_loss: %.4f - val_acc: %.4f' % (logs['loss'], logs['acc'], val_loss, val_acc))

input_shape = (224, 224, 3)
(x_train, y_train), (x_test, y_test) = cifar10.load_data()

x_train = Upscaling_Data(x_train, input_shape)
x_test = Upscaling_Data(x_test, input_shape)

x_train = np.float32(x_train / 255.)
x_test = np.float32(x_test / 255.)

y_train = to_categorical(y_train, num_classes=10)
y_test = to_categorical(y_test, num_classes=10)

model_input = Input( shape=input_shape )

model = plain18(model_input, 10)
#model = ResNet18(model_input, 10)
#model = ResNet50(model_input, 10)

validation_split = 0.2
batch_size = 256
iteration = 600000
epochs = round( (batch_size*iteration) / (len(x_train)*(1-validation_split)) )
optimizer = SGD(lr=0.1, decay=0.0001, momentum=0.9)
callbacks_list = [stop_on_iteration(iteration), ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=1)]

model.compile(optimizer, 'categorical_crossentropy', ['acc'])

model.fit(x_train, y_train, batch_size=256, epochs=epochs, validation_split=validation_split, callbacks=callbacks_list)

Keras의 iteration 단위로 구현하려면 train_on_batch() 함수를 사용하는게 정석이지만, 귀찮기 때문에 callback으로 구현했다.

물론 실험 PC의 스펙이 좋지 않은 이상, 이 크기의 입력을 batch_size=256으로 돌리려 한다면 OOM을 보게 될 것이다.

4.2 CIFAR10 and Analysis

논문에서는 CIFAR-10 dataset에 대한 더 많은 연구를 수행했다. training set에 대한 학습과 test set에 대한 평가를 기준으로 했으며, 이 연구는 extremely deep network에 초점을 둔 연구이기에 다음과 같이 총 6n+2개의 stacked weighted layer로 구성된 간단한 architecture를 사용했다.

• input은 per-pixel mean subtracted 32x32 이미지이다.

• 첫 번째 layer는 3x3 conv layer이다.

• 다음에는 크기가 각각 {32, 16, 8}인 feature map에 3x3 conv가 적용된 6n개의 layer stack을 사용한다. 각 size마다 2n개의 layer로 구성된다.

• filter의 수는 각각 {16, 32, 64}개 이다.

• subsampling은 strides가 2인 conv layer로 수행한다.

• 네트워크의 종단에는 global average pooling과 softmax를 포함한 FC layer로 구성된다.

• shortcut connection은 모두 identity shortcut로, 구조상 차이를 제외하고는 parameter 등의 모든 조건이 plain network와 동일하다.

학습 진행법은 다음과 같다.

• 4개의 pixel이 각 side에 padding되며, padded image와 horizontal flip 중에서 무작위로 32x32 crop을 샘플링 한다.

• He initialization으로 weight 초기화를 수행한다.

• decay는 0.0001, momentum은 0.9이다.

• learning rate는 0.1부터 시작하여 32000/48000번 째 iteration에서 rate를 10으로 나누어 적용한다.

• 2개의 GPU에서 mini-batch size를 128로 했으며, 총 64000번의 iteration 동안 학습한다.

• 성능 테스트 시에는 32x32의 원본 이미지에 대한 single view만 평가한다.

본 실험에서는 n = {3, 5, 7, 9}에 대한 20/32/44/56-layer network를 비교한다. Fig.6의 왼쪽은 이에 해당하는 plain network의 학습 결과이다. ImageNet에서와 마찬가지로 depth가 높아질 수록 성능이 하락하는 현상이 보이며, 이는 optimization difficulty가 특정 dataset에만 국한된 것이 아닌 본질적인 문제임을 시사한다.

Fig.6의 가운데는 ResNet의 학습 결과이다. 마찬가지로 ImageNet의 경우와 유사하게 depth가 증가할수록 정확도가 올라가는 결과이며, optimization difficulty를 극복하는 것으로 보인다.

Fig.6
각 결과는 CIFAR-10 dataset에 대한 학습 결과를 나타낸다. 왼쪽은 20/32/44/56-layer plain network의 학습 결과이며, 가운데는 20/32/44/56/110-layer ResNet의 학습 결과, 오른쪽은 110/1202-layer ResNet의 학습 결과이다.

얇은 곡선과 굵은 곡선은 각각 training error와 testing error이다.

추가로 n=18인 110-layer ResNet도 실험했다. 이 경우에는 수렴을 시작하기에 초기 learning rate가 0.1인 것이 약간 큰 것으로 나타났고, training error가 80% 이하가 될 때까지(약 400회의 iteration)는 rate를 0.01로 사용하고, 이후에는 0.1로 학습을 계속했다. 나머지 학습 일정은 20/32/44/56-layer의 경우와 동일하다. 이 네트워크는 잘 수렴했으며, FitNet과 Highway와 같은 deep and thin network보다 parameter의 수가 적음에도 state-of-the-art 결과 중 하나로 나타났다(Table.6 참조).

Table.6
CIFAR-10 test set에 대한 error를 나타낸다. 모든 결과는 data augmentation을 포함하여 학습한 모델의 결과이다. ResNet-110의 경우에는 5번 수행하여 나온 결과들의 ‘best(mean ± std)’ 를 나타낸 것이다.

Analysis of Layer Responses
Fig.7은 layer response의 std(standard deviation)를 나타낸다. response는 batch normalization과 nonlinearity(ReLU/addition) 사이에서의 각 3x3 conv layer의 output이다.

Fig.7
각 layer response들의 std를 그래프로 나타낸다. 위의 그래프는 각 layer의 순서대로 response의 std를 나타낸 것이며, 아래의 그래프는 response의 std를 내림차순으로 정렬하여 나타낸 것이다.

ResNet의 경우, 이 분석에서 residual function의 response 강도가 드러난다. Fig.7에서는 ResNet이 이에 대응하는 plain network보다 일반적으로 작은 response를 보여준다. 이는 residual function이 non-residual function보다 일반적으로 0에 가까울 것이라는 저자들의 basic motivation을 받쳐주는 결과이다. 또한, Fig.7을 통해 ResNet의 depth가 깊을 수록 더 작은 response를 보이는 것을 알 수 있다.

residual function의 response가 0에 가깝다고 예상하는 것은 다음 주장에 기인한다.

3.1절에서 설명한 바와 같이 optimal이 0보다 identity에 가깝다면 reformulation 식인 F + x에서 x를 기준으로 optimal을 찾게 될 것이므로, residual function인 F는 x로부터 optimal이 되기 위한 작은 변화량만을 학습하면 되기 때문이다.

depth가 깊어짐에 따라 response가 작아지는 현상은, 각 layer가 학습 시에 signal을 변화하는 정도가 작아지는 경향이 있음을 나타낸다.

Exploring Over 1000 layers
이제 1000개 이상의 layer로 구성된 aggressively deep model을 탐구한다. n=200인 1202-layer ResNet을 구성하고, 위와 동일한 방법으로 학습을 진행한다. 이 역시 optimization difficulty가 관찰되지 않았으며, 0.1% 미만의 traning error를 달성했으며, tesr error 역시 상당히 양호한 결과를 보였다(Fig.6 오른쪽 참조).

하지만, 이와 같은 aggressively deep model에 대해서는 여전히 문제가 있다. 이 모델은 110-layer ResNet과 비슷한 training error를 보였음에도, test 성능이 110-layer ResNet에 비해 뒤떨어진 것으로 나타났다. 저자들은 이 결과가 overfitting 때문이라 주장하고 있다. CIFAR-10과 같은 소규모 dataset에는 1202-layer ResNet(19.4M param)과 같은 모델이 불필요하게 큰 것으로 생각되기 때문이다.

또한, 이 논문에서는 maxout이나 dropout과 같은 강력한 regularization 기법을 사용하지 않았으며, 이와 같은 기법을 결합한다면 향상된 결과를 얻어낼 수 있을거라 생각된다.

---

2019-08-14 수정

Keras 구현에서 60K iteration만큼 동작하도록 callback 함수 구현

2019-10-05 수정

Keras 구현에서 bottleneck layer의 코드 가독성을 위해 일부 수정

2020-09-16 수정

ResNet18 구현 코드의 오타 수정